정규화란?
데이터베이스에서의 정규화는 중복 데이터를 최소화하고 무결성을 최대화하기 위한 설계 기법입니다.
정규화를 통해 효과적으로 설계된 데이터베이스는 업데이트 시 발생할 수 있는 문제를 줄이며, 데이터를 효율적으로 저장하게 됩니다.
무결성이란?
무결성(integrity)은 데이터베이스 관리 시스템(DBMS)에서 데이터의 정확성, 일관성 및 신뢰성을 유지하기 위한 속성을 의미합니다.
데이터베이스의 무결성을 유지하는 것은 중요한 설계 원칙 중 하나로, 데이터의 품질을 보장하며 애플리케이션의 신뢰성을 향상시킵니다.
- 도메인 무결성(Domain Integrity)
- 각 필드에 저장될 수 있는 값의 유형, 형식, 범위 및 가능한 값을 정의하며, 이에 따라 데이터가 저장되는지 확인합니다.
- 예를 들어, 나이 필드에 문자열이 들어가지 않도록하거나 날짜 형식이 'YYYY-MM-DD' 형식을 따르도록 하는 것입니다.
- 개체 무결성(Entity Integrity)
- 각 테이블의 기본 키(primary key)는 고유해야 하며, NULL 값을 허용하지 않아야 합니다.
- 이를 통해 테이블의 각 레코드를 고유하게 식별할 수 있습니다.
- 참조 무결성(Referential Integrity)
- 외래 키(foreign key)는 다른 테이블의 기본 키를 참조합니다.
- 참조 무결성은 외래 키 값이 참조하는 테이블의 기본 키 값 중 하나와 일치하거나 NULL 이어야 함을 보장합니다.
- 즉, 잘못된 참조나 존재하지 않는 데이터를 방지하는 데 중요합니다.
- 사용자 정의 무결성(User-defined Integrity)
- 데이터베이스 설계자나 애플리케이션 개발자가 특정 비즈니스 규칙에 따라 정의한 무결성 규칙입니다.
- 예를 들어, "고객의 할인율은 0%에서 50% 사이어야 한다"와 같은 규칙이 될 수 있습니다"
정규화 단계
1. 제1정규형 (1NF)
- 모든 속성은 원자값(더 이상 분해할 수 없는 값)을 가져야 합니다.
- 각 속성마다 고유한 값을 가져야 합니다.
1) 복합 속성(Composite Attributes)
- 속성이 여러 하위 속성으로 구성될 수 있는 경우가 있습니다.
- 예를 들어, '주소'라는 속성이 '도시', '주', '우편번호'와 같은 여러 하위 속성으로 나뉘어진다면, '주소'는 원자값이 아닙니다.
- 제 1정규형을 충족하기 위해 이러한 복합 속성을 각각의 독립적인 속성으로 분해해야 합니다.
2) 다중값 속성(Multi-valued Attributes)
- 하나의 속성이 여러 개의 값을 가질 수 있는 경우, 이 속성은 원자값이 아닙니다.
- 예를 들어, '전화번호'라는 속성이 사용자의 집, 사무실, 핸드폰 등 여러 번호를 가질 수 있다면, 이는 원자값이 아닌 다중값 속성입니다.
- 이러한 다중값 속성은 제 1정규형을 만족시키기 위해 별도의 테이블로 분리하거나 다른 방법으로 처리해야 합니다.
3) 중복 속성
- 하나의 엔터티 내에서 같은 정보를 중복해서 저장하는 것은 피해야 합니다.
- 예를 들어, '제품명'과 '제품 설명'이라는 두 개의 다른 속성에 같은 내용이 저장된다면, 이는 중복성을 초래하므로 제 1정규형을 위반하는 것입니다.
2. 제2정규형 (2NF)
- 제 1정규형을 만족해야 합니다.
- 기본 키가 아닌 모든 속성이 기본 키 전체에 함수적 종속되어야 합니다.
- 즉, 부분적 종속이 존재하지 않아야 합니다.
1) 함수적 종속(Functional Dependency)
- 속성 A의 값이 속성 B의 값을 유일하게 결정할 때, B는 A에 함수적으로 종속된다고 합니다(기호로는 A -> B)
- 예를 들면 "학번"이 "학생 이름"을 유일하게 결정하면 "학생 이름"은 "학번"에 함수적으로 종속되어 있습니다.
2) 부분적 종속(Partial Dependency)
- 복합 기본 키(둘 이상의 속성으로 구성된 키)를 가진 테이블에서 발생하는 종속 형태입니다.
- 만약 복합 기본 키의 일부만으로 다른 속성이 결정된다면, 그 속성은 부분적으로 종속되어 있다고 말합니다.
예를 들어 학생수강정보라는 테이블이 아래와 같이 있다고 하겠습니다.

이 테이블에서 기본 키는 '학번'과 '과목코드'의 조합입니다.
그런데 이 테이블을 살펴보면
'학생 이름'(StudentName)은 '학번'(StudentID)에만 종속되어 있습니다.
즉, '학번'만 알면 '학생이름'을 알 수 있습니다.
'과목명'(CourseName)은 '과목코드'(CourseCode)에만 종속되어 있습니다.
이러한 관계로 인해 김철수 학생이 두 과목을 수강하는 경우 '학생이름'이 두 번 중복되어 저장됩니다.
이런 부분적 종속을 해결하기 위해 제2정규형(2NF)을 적용하여 테이블을 분해합니다.
- 학생테이블

- 과목테이블

- 학생수강정보테이블

3. 제3정규형 (3NF)
- 제2정규형을 만족해야 합니다.
- 기본 키가 아닌 모든 속성이 기본 키에만 함수적 종속되어야 합니다. 이는 전이적 종속이 존재하면 안 된다는 것을 의미합니다.
전이적 종속(Transitive Dependency)
- 속성 A가 속성 B에 함수적으로 종속되고, 속성 B가 속성 C에 함수적으로 종속될 때, 속성 A도 속성 C에 함수적으로 종속되는 것을 의미합니다.
- 기호로 표현하면 A -> B, B -> C 가 동시에 참일 때, A -> C 도 참인 경우입니다.
예시) 고객 주문 정보

이 테이블에서 '제품분류'(Category)는 '제품ID'(ProductID)에 함수적으로 종속되어 있습니다.
그러나 '제품ID'는 '주문ID'에 함수적으로 종속되어 있습니다.
따라서 '제품분류'는 '주문ID'에 전이적으로 종속된 상태입니다.
이를 해결하기 위해 제3정규형을 적용하여 테이블을 분리합니다.
- 주문 테이블

- 제품 테이블

이렇게 테이블을 분리하면 전이적 종속 문제가 해결되며, 각 테이블의 역할이 명확해집니다.
또한, 제품의 분류정보를 업데이트할 때는 제품 테이블만 변경하면 되므로 데이터 관리가 보다 효율적입니다.
4. BCNF (Boyce-Codd Normal Form)
- 제3정규형을 만족해야 합니다.
- 모든 결정자는 후보 키의 부분집합이어야 합니다.
결정자, 후보키, 기본키 설명
예시) 학생과 강의를 관리하는 테이블

1) 결정자(Determinant)
- '강의코드'는 '강의명'을 결정합니다. 즉, '강의코드'가 주어지면 해당 강의의 이름을 알 수 있습니다.
- 따라서 '강의코드'는 강의명'의 결정자입니다('강의코드' -> '강의명')
2) 후보키(Candidate Key)
- '(학번, 강의코드)'의 조합은 테이블의 각 튜플을 유일하게 식별합니다.
- 다른 조합으로는 튜플을 유일하게 식별할 수 없습니다.
- 따라서 '(학번, 강의코드)'의 조합이 후보키입니다.
3) 기본키(Pirmarty Key)
- 위에서 언급한 후보키 '(학번, 강의코드)' 중에서 우리가 실제 데이터베이스 설계시에 기본키로 선택한 키를 말합니다.
- 여기서는 '(학번, 강의코드)'만이 유일하게 튜플을 식별할 수 있는 후보키이므로 해당 키만이 기본키로 선택할 수 있습니다.
- 이 기본키에 의해 각 튜플은 고유하게 식별됩니다.
모든 결정자는 후보 키의 부분집합이어야 합니다.
예시) 대학생과 선택한 전공

이 테이블에서는 '전공명'이 '담당 교수'를 결정합니다.
즉 '전공명 -> 담당 교수' 라는 함수적 종속성이 존재합니다.
하지만, '전공명'은 이 테이블의 후보키가 아닙니다. 왜냐하면 '전공명'만으로는 각 튜플(레코드)을 구별할 수 없기 때문입니다.
'학번' 혹은 '학번 + 전공명' 조합이 후보키가 될 수 있습니다.
이 경우, '전공명' 이 결정자이지만 후보 키의 부분집합이 아닙니다.
따라서 이 테이블은 BCNF를 만족하지 않습니다.
BCNF를 만족시키기 위해 분해
1) 학생과 전공 테이블

2) 전공과 담당 교수 테이블

5. 제4정규형(4NF)
- BCNF를 만족해야 합니다.
- 다중값 종속성이 없어야 합니다.
다중값 종속성(MVC, Multi-Valued Dependency)
- 릴레이션 R의 두 속성 A와 B에 대해, A의 어떤 값을 가지는 튜플들이 B의 값을 독립적으로 가질 수 있을 때 발생합니다.
- 기호로는 A ->> B 라고 표현합니다.
예시) 학생들이 참여하는 동아리와 스포츠 활동

이 테이블에서 주요 포인트는 '학생이름' 속성에 대한 다른 두 속성 ('동아리'와 '스포츠') 사이의 독립적인 관계입니다.
데이터를 보면 '지민'이 '미술' 동아리와 '음악' 동아리에 동시에 속하고 있으며, 동시에 '농구'와 '축구' 스포츠 활동에 참여하고 있습니다.
이때, '지민'의 '미술' 동아리 참여는 '농구'나 '축구' 활동과 직접적인 연관이 없습니다.
즉, '동아리' 참여와 '스포츠' 활동은 독립적인 관계를 가지고 있습니다.
다중값 종속성은 이런 독립적인 관계 때문에 발생합니다.
'학생이름'에 대해 '동아리'와 '스포츠'의 관계가 독립적으로 존재하므로 '학생이름'이 '동아리'에 대한 다중값 종속성과 '스포츠'에 대한 다중값 종속성을 모두 갖게 됩니다.
다시 말하면, '지민'이 참여하는 '동아리'는 '지민'이 참여하는 '스포츠'에 의해 영향을 받지 않습니다.
이는 '학생이름 ->> 동아리'와 '학생이름 ->> 스포츠'의 두 개의 다중값 종속성을 나타냅니다.
이러한 다중값 종속성을 해결하기 위해 테이블을 분리 하면 다음과 같습니다.
1) 학생과 동아리 테이블

2) 학생과 스포츠 테이블

6. 제5정규형(5NF 또는 PJNF, Project-Join Normal Form)
- 제4정규형을 만족해야 합니다.
- 조인 종속을 고려하여 분해하였을 때 원래의 관계를 복원할 수 있어야 합니다.
조인 종속(Join Dependency)란?
조인 종속은 릴레이션 R을 두 개 이상의 릴레이션 R1, R2, ..., Rn 으로 분해한 후, 이들을 다시 조인했을 때 원래의 릴레이션 R을 복원할 수 있을 때 발생합니다.
기호로는 R = R1 ⨝ R2 ⨝ ... ⨝ Rn과 같이 나타낼 수 있습니다.
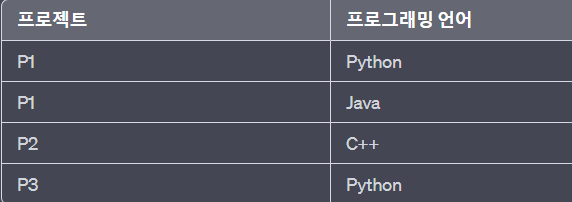
예시) 학생이 참여하는 프로젝트와 해당 프로젝트에서 사용하는 언어를 나타내는 테이블

이 테이블을 다음과 같이 두 개의 릴레이션으로 분해합니다.
- 릴레이션 R1

- 릴레이션 R2
이제 R1과 R2를 조인하면 원래의 릴레이션을 복원할 수 있습니다.
이 경우, 원래의 릴레이션에 대한 조인 종속이 발생하며, 이 릴레이션은 5NF를 만족합니다.
제5정규형의 주요 목적은 릴레이션을 적절하게 분해하여 데이터 중복을 제거하면서도 조인 연산을 통해 원래의 릴레이션을 손실 없이 복원할 수 있도록 하는 것입니다.